How To Use Simpson's Rule

Simpson's Rule: the Formula and How it Works

Simpson'south rule is a method for numerical integration. In other words, it's the numerical approximation of definite integrals.

Simpson'southward dominion is equally follows:

In it,

f(ten) is called the integrand
a = lower limit of integration
b = upper limit of integration

Simpson's 1/3 Dominion

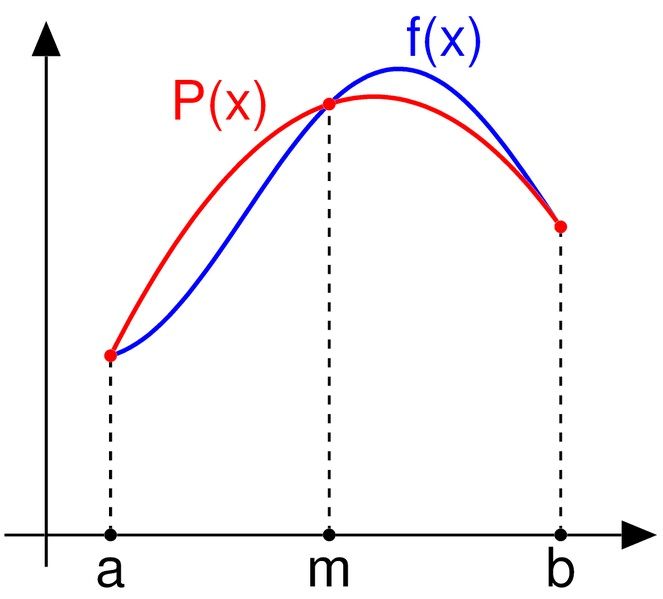
As shown in the diagram in a higher place, the integrand f(10) is approximated past a second order polynomial; the quadratic interpolant being P(ten).

The approximation follows,

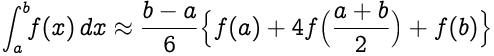
Replacing (b-a)/two as h, we get,

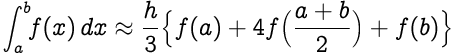
Equally you lot can see, in that location is a factor of 1/3 in the above expression. That's why, it is called Simpson's one/3 Dominion .

If a function is highly oscillatory or lacks derivatives at certain points, so the above dominion may fail to produce accurate results.

A common way to handle this is by using the blended Simpson's rule arroyo. To do this, break upward [a,b] into pocket-sized subintervals, so employ Simpson's rule to each subinterval. And so, sum the results of each adding to produce an approximation over the entire integral.

If the interval [a,b] is separate into n subintervals, and n is an even number, the composite Simpson's dominion is calculated with the following formula:

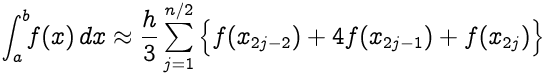
where x_j = a+jh for j = 0,one,…,northward-1,north with h=(b-a)/n ; in particular, x₀ = a and x_n = b .

Example in C++:

To guess the value of the integral given beneath where n = viii:

                #include<iostream> #include<cmath> using namespace std;  float f(float ten) { 	return x*sin(x);	//Define the part f(x) }  float simpson(float a, float b, int n) { 	bladder h, x[n+i], sum = 0; 	int j; 	h = (b-a)/n; 	 	10[0] = a; 	 	for(j=1; j<=north; j++) 	{ 		ten[j] = a + h*j; 	} 	 	for(j=1; j<=north/two; j++) 	{ 		sum += f(x[ii*j - 2]) + four*f(10[two*j - 1]) + f(x[2*j]); 	} 	 	render sum*h/three; }  int master() { 	float a,b,northward; 	a = 1;		//Enter lower limit a 	b = 4;		//Enter upper limit b 	n = 8;		//Enter step-length n 	if (north%2 == 0) 		cout<<simpson(a,b,due north)<<endl; 	else 		cout<<"n should be an even number"; 	return 0; }

Simpson's 3/8 Dominion

Simpson'due south 3/8 rule is similar to Simpson's ane/3 rule, the but departure being that, for the 3/viii rule, the interpolant is a cubic polynomial. Though the 3/8 rule uses one more than office value, it is about twice equally accurate as the 1/3 rule.

Simpson's 3/8 dominion states :